Inverse Kinematics for Serial Kinematic Chains via Sum of Squares Optimization

arXiv pre-print View it on Github DOI

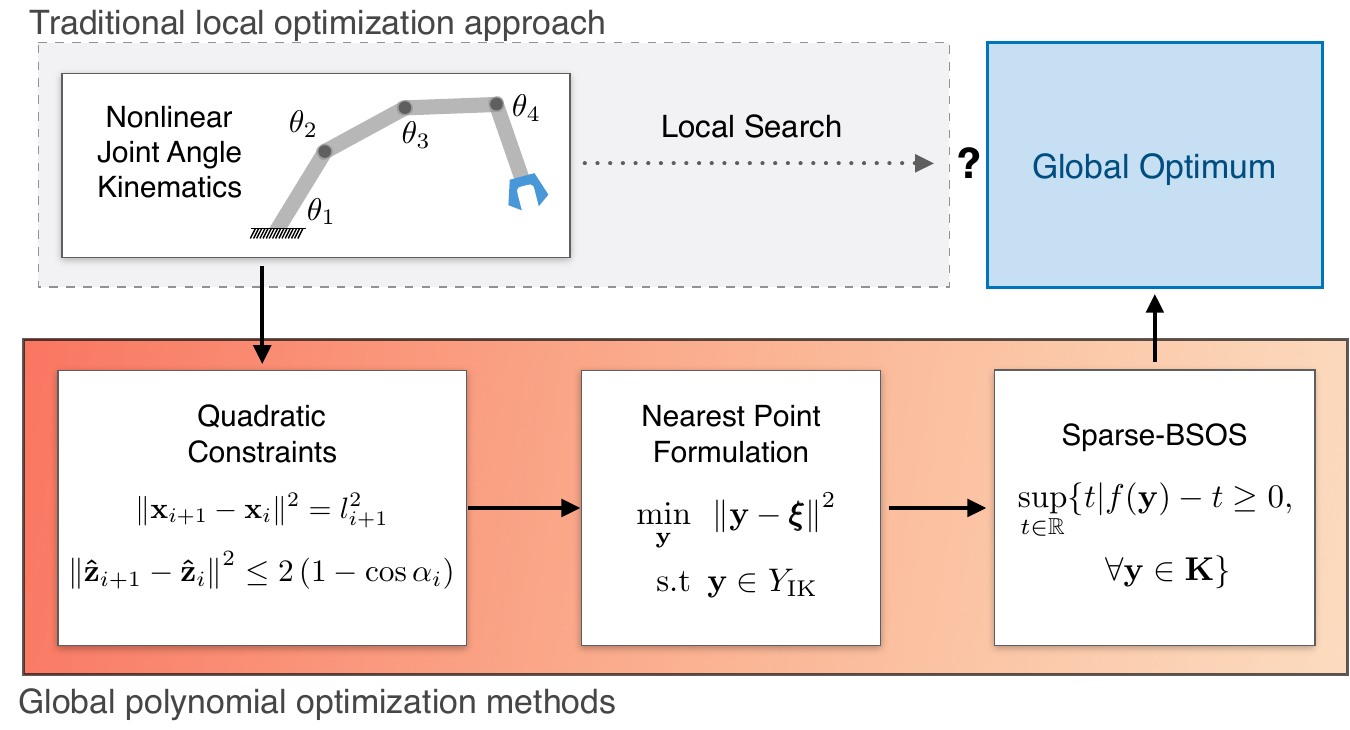
In this paper, we use convex optimization techniques to solve the inverse kinematics problem with joint limit constraints for highly redundant serial kinematic chains with spherical joints in two and three dimensions. This is accomplished through a novel formulation of inverse kinematics as a nearest point problem, and with a fast sum of squares solver that exploits the sparsity of kinematic constraints for serial manipulators. Our method has the advantages of post-hoc certification of global optimality and a runtime that scales polynomialy with the number of degrees of freedom. Additionally, we prove that our convex relaxation leads to a globally optimal solution when certain conditions are met, and demonstrate empirically that these conditions are common and represent many practical instances.

Video

Abstract

Inverse kinematics is a fundamental problem for articulated robots: fast and accurate algorithms are needed for translating task-related workspace constraints and goals into feasible joint configurations. In general, inverse kinematics for serial kinematic chains is a difficult nonlinear problem, for which closed form solutions cannot be easily obtained. Therefore, computationally efficient numerical methods that can be adapted to a general class of manipulators are of great importance. % to motion planning and workspace generation tasks. In this paper, we use convex optimization techniques to solve the inverse kinematics problem with joint limit constraints for highly redundant serial kinematic chains with spherical joints in two and three dimensions. This is accomplished through a novel formulation of inverse kinematics as a nearest point problem, and with a fast sum of squares solver that exploits the sparsity of kinematic constraints for serial manipulators. Our method has the advantages of post-hoc certification of global optimality and a runtime that scales polynomialy with the number of degrees of freedom. Additionally, we prove that our convex relaxation leads to a globally optimal solution when certain conditions are met, and demonstrate empirically that these conditions are common and represent many practical instances. Finally, we provide an open source implementation of our algorithm.

Citation

@inproceedings{2020_Maric_Inverse,
  address = {Paris, France},
  author = {Filip Maric and Matthew Giamou and Soroush Khoubyarian and Ivan Petrovic and Jonathan Kelly},
  booktitle = {Proceedings of the {IEEE} International Conference on Robotics and Automation {(ICRA)}},
  date = {2020-05-31/2020-06-04},
  doi = {10.1109/ICRA40945.2020.9196704},
  month = {May 31--Jun. 4},
  title = {Inverse Kinematics for Serial Kinematic Chains via Sum of Squares Optimization},
  url = {http://arxiv.org/abs/1909.09318},
  video1 = {https://www.youtube.com/watch?v=AdPze8cTUuE},
  year = {2020}
}

---